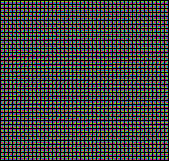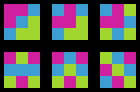Some Squares
Just now I was in the need of redecorating my bathroom window.
It is made of nine square glass bricks arranged neatly in a 9x9 grid. So I grabbed a pen and a sheet of paper and started to draw some stuff in the fashion of the aforementioned grid.
Soon I realized that there are quite a number of possible combinations to arrange nine different things on nine different fields. 9*8*7*6*5*4*3*2*1 = 362880 to be precise. That's a lot for a little pencil and a short human lifespan. But what am I a programmer for? Just trot out some code and make a dumb but fast computer do all the drawing. And here is the result:

All 362880 combinations of nine different colors, each one on a 9x9 pixel area.
There are 630x576 3x3 squares which results in a 2521x2305 pixel image.
(footnote)
You can click it to see the image in full size.
Thats quite a load. But if we take a closer look we just see some random distribution of colors. We could just as well throw dice to determine one of these arrangements. That's a bit boring.

The first seven squares from the image above.
Come to think of it, there is no order without some kind of repetition. So instead of just painting each cell in a different color, I chose to limit myself to three colors with each color occupying three fields. Maybe there are interesting patterns awaiting by not giving each color the same amount of space or if one would choose 2 or 4 colors, but I leave that for a later experiment.

All 362880 combinations of 3x3 different colors, each one on a 9x9 pixel area.
There are still 630x576 3x3 squares which obviously results in a 2521x2305 pixel image.
Again you can click it to see it's entireness.
Since there are still 9 fields in each square there are still 362880 combinations. But something must have changed, so lets look at the first seven squares again:

The first seven squares from the previous image.
Whoopsie, most of them look the same. And there are more of these later on. Well, some math reveals that there are actually 63 = 216 ways to arrange 3x3 colors on a 9x9 grid that all look the same. That means there are only 362880 / 216 = 1680 different squares remaining:
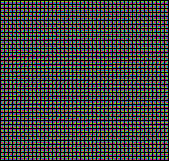
All 1680 permutations of 3x3 colors, without duplicates.
No link to a big picsh, thats all there is, neatly arranged on a 42 by 40 grid.
Looks good. Still a lot, though. And a bit small, so here are the first seven again:

The first seven squares from the previous image.
But wait! Do you notice anything special about the 2nd and 6th square in the previous image? No? What about the following 48 squares? They all can be found in the 42x40 grid above.

48 permutations which look somehow conspicuous in what way?
Still not? May these twelve ones rings a bell:

Now, there is some similarity!
Okay, Here it is: They are all different but they all represent the same pattern, only rotated, mirrored or with exchanged colors. So for my purpose (find out how many different options I have to decorate my bathroom window) they can be regarded as equal and removed from the list (except one of course).
Interestingly there remain only 42 distinct variations:

42 permutations, none of which can be transformed into another one by rotating, flipping horizontally or vertically or by exchange of colors.
But which one to choose? Lets see, six of these have another interesting property: They are symmetric.
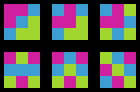
Permutations that are mirror-symmetric with respect to a vertical or diagonal axis.
The last one (bottom right) has another nice quality: The colors are distributed as even as possible. Each 4x4 subsquare contains all three colors and each 3x2 sub-rectangle contains each color twice. Also there are no same colors next to each other. Since I spent way too much time with this already I just pick that one.

There we are. Isn't it beautiful?
Now I only have to decide what to put on my bathroom window actually. Some color patches? Images of dental hygiene products? Photographs of nude people? Well, something will turn up. At least I found a nice occurrence of the number 42.
Interesting note aside: The file size of this image file is 16 MB when uncompressed, about 10MB with high quality JPEG compression, 1.6 MB with low quality JPEG (very bad,alost unrecognizable) and 500 KB with PNG compression, which is perfectly lossless. The lesson in there for all of us: Know your compression algorithm and choose wisely depending on your source image.